В экономической действительности на каждом шагу встречаются ситуации, когда отдельные люди, фирмы или целые страны пытаются перехитрить друг друга в борьбе за первенство. Олигополии, которые мы анализировали ранее, также подчас ввязываются в экономические войны. Именно такими ситуациями и занимается ветвь экономического анализа, называемая лтеория игр╗.

Теория игр изучает то, каким образом двое или более игроков выбирают отдельные действия или целые стратегии. Название этой теории настраивает на несколько отвлеченный лад, поскольку оно ассоциируется с игрой в шахматы и бридж или с ведением войн. На самом деле, выводы этой дисциплины весьма глубоки. Теория игр была разработана выходцем из Венгрии, гениальным математиком Джоном фон Нейманом (1903-1957). Мы дадим беглую характеристику основных понятий этой теории и обсудим некоторые ее важные приложения к экономике.

Начнем с рассмотрения процесса взаимного сбивания цены. Допустим, вы Ч глава одного из универмагов лСеменов╗, расположенного в Москве. Ваш лозунгЧлДешевле не бывает╗. Ваш коварный соперник, лПетров╗, ведет рекламную компанию под девизом лНаши цены на 10% ниже╗. Рис. 1 иллюстрирует, как будут развиваться события. Вертикальные стрелки изображают динамику цен лПетрова╗. Горизонтальные Ч ваши ответные действия на каждое понижение.

Рис. 1. Что происходит, когда две фирмы конкурируют друг с другом посредством снижения цен

Проследите стадии, через которые проходит динамический процесс снижения цен двух соперничающих между собой фирм

Проследив за всеми действиями и контрдействиями, вы увидите, что данный вид соперничества приведет к взаимному уничтожению при нулевой цене. Почему? Потому, что только такая цена совместима с обеими стратегиями: 90% от ноля все тот же ноль.

Наконец, вы осознаете, что, когда вы понижаете цены, лПетров╗ отвечает тем же. Нужно быть совершенно близоруким, чтобы не понимать, чем окончатся ваши игры. Поэтому вы начнете задумываться, как отреагирует лПетров╗, если вы назначите цену А, цену В, и т.д. Приступив к размышлениям на эту тему, вы сделаете первый шаг в теории игр.

Базовые понятия теории игр

Мы начнем с того, что продемонстрируем главные положения теории игр, рассмотрев ценовую войну при дуополии. Итак, пусть две фирмы должны решить, вступить ли им в ценовую войну. Простоты ради, мы предположим, что обе фирмы имеют одинаковые издержки и структуру спроса. Пусть также каждая фирма стоит перед выбором, установить ли нормальную цену или понизить ее ниже уровня предполагаемых издержек и таким образом привести к банкротству своего соперника. Характерная черта этой ситуации состоит в том, что прибыль каждой фирмы зависит от стратегии соперника в той же степени, что и от своего собственного поведения.

Удобно представить взаимодействие между двумя фирмами или индивидами с помощью таблицы (матрицы) выигрышей для двух игроков. В такой таблице перечислены стратегии двух игроков и соответствующие выигрыши. Рис. 2 иллюстрирует ценовую войну между двумя универмагами. Фирма может принять одну из стратегий, выбрав соответствующий столбец или строку. К примеру, лПетров╗ может выбрать между двумя столбцами, лСидоров╗Чмежду двумя строками. В нашем случае каждая фирма должна решить, назначить ли нормальную цену или развязать ценовую войну, понизив цену.

Четыре возможных сочетания действия и контрдействия дают четыре возможных исхода, отображенных в ячейках матрицы. Ячейка А (слева вверху) представляет ситуацию, когда обе фирмы выбрали нормальную цену. Исход D подразумевает, что обе фирмы решили открыть военные действия. Исходы В и С возникают, когда одна из фирм не захотела вступить в конфликт, а другая на это решилась.

Числа в ячейках Ч это выигрыши или прибыли, с которыми остается та или иная фирма при определенном исходе (цифры в левом нижнем углу каждой ячейки относятся к лСидорову╗, а в правом верхнем углу Ч к лПетрову╗). Поскольку фирмы находятся в равных условиях, существует соответствие между выигрышами обеих фирм.

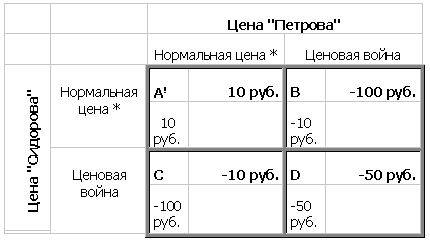
* - Доминирующая стратегия

! - Доминирующее равновесие

Рис. 2. Таблица выигрышей при ценовой войне

Таблица выигрышей показывает прибыль универмагов при различных стратегиях. "Сидоров" стоит перед выбором между двумя стратегиями, представленными в двух строках таблицы. Двум стратегиям "Петрова" соответствуют два столбца. Цифры в ячейках означают прибыли игроков. К примеру, "Сидоров" выбирает стратегию лценовая война╗, а "Петров" Чстратегию лнормальная цена╗. Результат отображен в ячейке С. лВыигрыш╗ "Сидорова" равен Ч 100 руб., лвыигрыш╗ "Петрова" равен Ч10 руб. Обсудив все варианты, можно прийти к выводу, что равновесие установится в ячейке А.

Альтернативные стратегии

Теперь, когда мы уяснили основные понятия теории игр, обсудим, как же должны поступать участники олигополии из двух фирм или участники любой другой игры. Мы по-прежнему предполагаем, что фирмы максимизируют прибыль, а потребители Ч полезность. Однако, в добавление к этому, теория игр выдвигает положение, что вы выбираете то или иное решение, исходя из анализа возможных действий вашего соперника. Но вам не нужно забывать, что этот последний также будет изучать ваши возможные стратегии. Таким образом, любое ваше решение основывается на допущении, что ваш соперник так же, как и вы, всегда заглядывает вперед и действует в собственных интересах.

Давайте приложим это правило к нашему примеру с олигополией из двух участников. Во-первых, заметим, что фирмы имеют наибольшую совместную прибыль при исходе А. Если обе компании придерживаются нормальной цены, то каждая получит по 10 руб. В противоположном углу (исход D) отображена ситуация ценовой войны (каждая фирма устанавливает низкие цены и терпит убытки). Между этими крайними ситуациями находятся другие две. К примеру, исход С означает, что лПетров╗ назначил нормальную цену, в то время как лСидоров╗ избрал конфронтацию. Хотя лСидорову╗ удается завладеть большей частью рынка, это дается ему ценой огромных убытков, и, в сущности, лПетров╗ оказывается в лучшем положении, продолжая продавать по прежней цене.

Доминирующая стратегия. Простейшим примером стратегии является так называемая доминирующая стратегия. Такое положение возникает, когда один из игроков обладает лучшей стратегией независимо от того, какой стратегии следуют другие игроки.

Рассмотрим, к примеру, какими возможностями располагаете вы, в качестве главы лСидорова╗. Допустим, лПетров╗ придерживается нормальной цены. Тогда, если вы также изберете мирную стратегию, то получите 10 рублей прибыли. Если же вы ступите на лтропу войны╗, то потеряете 100 рублей. Если же лПетров╗ назначает заниженную цену, то вы в любом случае потерпите убытки Ч в 50 рублей, если последуете примеру лПетрова╗, и в 10 рублей, если поступите наоборот. Те же самые рассуждения применимы и к лПетрову╗, поскольку и вы, и он находитесь в равных условиях. Следовательно, для любой из фирм разумнее всего придерживаться нормальной цены, вне зависимости от того, какую стратегию избрала другая фирма. Сохранение нормальной цены является доминирующей стратегией для обеих фирм в этой ценовой войне.

Если у каждого из игроков имеется доминирующая стратегия, то исходом такой игры будет доминирующее равновесие. Несложно заметить, что в нашей игре доминирующее равновесие представлено ячейкой А (рис. 11-3). Именно этот исход возникает, если обе фирмы будут держаться своих доминирующих стратегий.

Равновесие по Нэшу. Однако существуют и более интересные ситуации, чем доминирующее равновесие. Вернемся к нашему примеру с двумя универмагами. Каждый из их владельцев должен ответить для себя на вопрос: сохранить ли ему прежнюю нормальную цену или же повысить ее до размеров монопольной, попытавшись тем самым получить сверхприбыль. В этом случае речь идет о так называемой конкурентной игре.

Чтобы лучше понять, в чем суть такой игры, обратимся к рис. 3. Фирмы имеют возможность отказаться от всяких попыток нарушить установившееся равновесие, сохраняя нормальные цены. Но они могут также попытаться поднять свои цены, чтобы получить монопольную прибыль. Для начала обратим внимание на то, что максимум общей прибыли достигается в ячейке А. При таком исходе магазины будут зарабатывать в совокупности 300 руб. Поведение фирм, назначивших высокие цены (ячейка А), не будет отличаться от действий монополии. Но фирмы могут избрать и противоположную линию поведения, назначив нормальные цены. Фирмы будут зарабатывать по 10 руб., и этот исход будет в большой степени напоминать результат деятельности конкурентного рынка.

Промежуточное положение между рассмотренными стратегиями занимают еще два возможных образа поведения. К примеру, ячейка А представляет случай, когда лПетров╗ назначает высокую цену, а лСидоров╗ решил лподставить ему ножку╗, придерживаясь прежней цены. лСидоров╗ остается в большом выигрыше, заняв лидирующее положение на рынке, в то время как лПетров╗ терпит убытки. В ячейке В лСидоров╗ отважился на высокую цену, однако более спокойное поведение лПетрова╗ обходится ему явными потерями.

В этой конкурентной игре лСидоров╗ имеет доминирующую стратегию, поскольку ему выгоднее всего держаться нормальной цены. А вот у лПетрова╗ нет доминирующей стратегии: если лСидоров╗ назначает нормальную цену, то и лПетрову╗ следует назначить нормальную, а если же лСидоров╗ изберет высокую цену, то для лПетрова╗ будет разумнее поступить так же. Перед лПетровым╗ стоит интересная дилемма. Он может поставить на высокую цену, рассчитывая, что лСидоров╗ сделает то же самое. Но он может избрать и нормальную цену. Если мы внимательно разберем все имеющиеся у лПетрова╗ возможности, то станет ясно, что ему следует назначить нормальную цену. Несложно понять, почему. Поставим себя на место главы лПетрова╗. Мы уже выяснили, что лСидоров╗, какую бы стратегию ни избрал лПетров╗, скорее всего выберет нормальную цену. Из нее-то и должен исходить лПетров╗. Следовательно, лПетров╗ должен назначить нормальную цену.

В итоге игроки придут к достаточно распространенной ситуации, которая называется равновесием по Нэшу (по имени математика Джона Нэша). Равновесие по Нэшу возникает, когда ни один из игроков не может улучшить своего положения, если его противники не изменят своих стратегий. То есть, если игрок А сохраняет свою стратегию, то игрок В не может выбрать стратегию, которая улучшила бы его положения, и то же самое относится к игроку А. Стратегия каждого игрока является лучшим ответом на стратегию его противника.

Рис. 3. Следует ли дуополисту устанавливать монопольную цену?

В условиях конкурентной игры каждая фирма может получить по 10 руб., придерживаясь нормальной цены. Если оба соперника повысят свои цены до монопольного уровня, то общая прибыль будет максимальной. Однако поскольку каждая фирма будет испытывать в этом случае большое искушение лсплутовать╗ и повысить свою прибыль, то, скорее всего, фирмам не удастся вступить в сговор и они окажутся в равновесии по Нэшу.

Иногда равновесие по Нэшу называют также некооперативным равновесием, поскольку участники совершают свой выбор, не вступая ни в какие соглашения друг с другом и не принимая во внимание никаких других соображений (интересы общества или интересы других сторон), кроме собственной выгоды.

Нетрудно убедиться, что исход, обозначенный звездочкой (рис. 3), является равновесием по Нэшу. В самом деле, ни лПетров╗, ни лСидоров╗ не могут выбрать лучшей стратегии, чем сохранение нормальной цены. Если лСидоров╗ решит назначить высокую цену, то вместо прибыли в 10 руб. он получит ущерб в 20 руб. Если же лПетров╗ попробует покинуть равновесие по Нэшу, то его убыток составит 30 руб. вместо прежних 10 руб. прибыли (убедитесь, что и равновесие на рис. 2 также является равновесием по Нэшу).

Теория игр

Несколько важных приложений теории игр

Вступать или не вступать в сговор?

Рис. 11-4 освещает важный факт. В ситуации равновесия по Нэшу (ячейка D) общая прибыль будет меньше, чем при любом другом исходе. С точки зрения совокупного выигрыша наибольшим преимуществом обладает исход в точке А. Здесь обе фирмы назначили высокую цену и получают 300 руб. общей прибыли. Хуже всего выглядит именно равновесие по Нэшу, с 20 руб. общей прибыли.

Почему же при таком, казалось бы, наименее выгодном положении, возникает равновесие? Обратимся к Адаму Смиту: лЛюди, занимающиеся одним и тем же делом, редко собираются вместе..., но, если подобное общение все же имело место, оно часто заканчивается договоренностью повысить цены╗. Почему бы нашим универмагам также не вступить в сговор и не поднять цены? На самом деле, они могут прекрасно договориться и начать действовать совместно, в полном согласии друг с другом, извлекая прибыль. Кооперативное равновесие возникает, когда несколько сторон совместными усилиями находят такую линию поведения, которая увеличивает их совокупную прибыль. Фирмы могут решить образовать картель, установив высокие цены и поровну деля прибыль. Ясно, что подобное благоденствие будет достигнуто за счет потребителей. В нашей конкурентной игре максимальная общая прибыль образуется в ячейке А.

Что мешает прийти к сговору? Во-первых, в большинстве стран с рыночной экономикой это запрещено. Но имеется и более глубокая причина. Некоторые участники картеля могут не устоять перед искушением смошенничать. Вернемся к ситуации в ячейке А (рис. 11-4). Здесь оба участника установили высокие цены. Но, если, скажем, лСидоров╗ тайно решил продавать некоторое количество товара по более низкой цене, и может сделать это так, что его новый партнер ничего не заметит, то он заработает даже больше, чем в положении кооперативного равновесия: 150 руб. (ячейка С) вместо 100 руб. (ячейка А).

Но, в действительности, управляющий лПетрова╗ скорее всего заметит, что его прибыль упала. Ему останется сделать вывод, что картель развалился, и опустить цены до нормального уровня. Поскольку кооперативное равновесие оказалось неустойчивым, то фирмы в конце концов возвратятся к равновесию в ячейке D.

Эти рассуждения приложимы и к конкурентному рынку. Равновесие совершенно конкурентного рынка также является равновесием по Нэшу, или некооперативным равновесием, при котором каждая фирма и каждый потребитель принимают решения, исходя из уже существующих цен, как не зависящих от его воли. Мы уже знаем, что в условиях, когда каждая фирма стремится максимизировать прибыль, а каждый потребитель Ч полезность, равновесие возникает, когда цены равны предельным издержкам, а прибыль Ч нулю.

Вспомним концепцию лневидимой руки╗ Адама Смита: лПреследуя собственные интересы, он (индивид) часто в большей степени способствует процветанию общества, чем если бы он к этому сознательно стремился╗. Парадокс лневидимой руки╗ заключается в том, что, хотя каждый и действует как самостоятельная сила, в конечном итоге, общество остается в выигрыше. При этом конкурентное равновесие является равновесием по Нэшу еще и в том смысле, что ни у кого нет повода изменять свою стратегию, если и все остальные придерживаются своей. В условиях совершенно конкурентной экономики некооперативное поведение является экономически эффективным с точки зрения интересов общества.

Напротив, когда члены некоторой группы (вспомним наши универмаги) решают кооперироваться и совместно прийти к монопольной цене (ячейка А) , такое поведение нанесет ущерб экономической эффективности. Государство вынуждено создавать антимонопольное законодательство и тем самым урезонивать тех, кто пытается завысить цены и поделить рынок.

Игра в загрязнение (окружающей среды)

Однако не всегда разобщенность в поведении является экономически эффективной. Теория игр может пролить свет на такие случаи. Мы видели (рис. 3), что соперничество между фирмами ведет к низким ценам и конкурентному объему производства. Более того, мы пришли к выводу, что лневидимая рука╗ оказывает почти волшебное воздействие на совершенно конкурентные рынки: эффективное распределение ресурсов происходит в результате действий индивидов, стремящихся к максимизации прибыли.

Однако во многих случаях некооперативное поведение приводит к экономической неэффективности или даже представляет угрозу для общества. Примечательный пример томуЧгонка вооружений. Некооперативное поведение, как со стороны США, так и со стороны СССР заставляло обе стороны вкладывать огромные средства в военную область и привело к созданию арсенала, состоящего из почти 100.000 ядерных боеголовок. Существует также опасение, что чрезмерная доступность оружия в Америке может стать причиной своего рода внутренней гонки вооружений. Одни люди вооружают себя против других Ч и этот лбег наперегонки╗ может продолжаться до бесконечности. Здесь в действие вступает вполне лвидимая рука╗, направляющая это разрушительное состязание и не имеющая ничего общего с лневидимой рукой╗ Адама Смита. Еще один важный экономический пример Ч игры в загрязнения (окружающей среды) (рис. 11 -5). Здесь объектом нашего внимания станет такой вид побочных эффектов, как загрязнение. Если бы фирмы никогда и никого не спрашивали о том, как им поступить, любая из них скорее предпочла бы создавать загрязнения, чем устанавливать дорогостоящие очистители. Если же какая-нибудь фирма из благородных побуждений решилась бы уменьшить вредные выбросы, то издержки, а следовательно и цены на ее продукцию, возросли бы, а спрос бы упал. Вполне возможно, эта фирма просто обанкротилась бы. Живущие в жестоком мире естественного отбора, фирмы скорее предпочтут оставаться в условиях равновесия по Нэшу (рис. 4, ячейка D). Ни одной фирме не удастся повысить прибыль, уменьшая загрязнение.

* - равновесие по Нэшу

Рис. 4. Некооперативное поведение ведет к увеличению загрязнения

Вступив в смертоносную экономическую игру, каждая неконтролируемая государством и максимизирующая прибыль сталелитейная фирма будет производить загрязнения воды и воздуха. Если какая-либо фирма попытается очищать свои выбросы, то тем самым она будет вынуждена повысить цены и потерпеть убытки. Некооперативное поведение установит равновесие по Нэшу в условиях высоких выбросов (ячейка D). Правительство может предпринять меры с тем, чтобы равновесие переместилось в ячейку А. В этом положении загрязнение будет незначительным, прибыли же останутся теми же

Игры загрязнения Ч один из случаев того, как механизм действия лневидимой руки╗ не срабатывает. Это ситуация, когда равновесие по Нэшу неэффективно. Иногда подобные неконтролируемые игры становятся угрожающими, и здесь может вмешаться правительство. Установив систему штрафов и квот на выбросы, правительство может побудить фирмы выбрать исход А, соответствующий низкому уровню загрязнения. Фирмы зарабатывают ровно столько же, сколько и прежде, при больших выбросах, мир же становится несколько чище.

Бюджетно-денежные игры

Теория игр применима и к макроэкономической политике. Экономисты и политики в США часто поругивают существующую денежно-кредитную и налогово-бюджетную политику: дефицит федерального бюджета слишком велик и уменьшает национальные сбережения, тогда как кредитно-денежная политика порождает такие процентные ставки, которые ограничивают инвестиции. Более того, этот лбюджетно-денежный синдром╗ является свойством макроэкономического лландшафта╗ уже более десяти лет. Почему же Америка так упорно проводит оба вида политики, хотя ни один из них не желателен.

Можно попытаться объяснить этот синдром с точки зрения теории игр. Стало привычным в современной экономике разделять данные разновидности политики. Центральный банк Америки Ч Федеральная резервная система Ч определяет независимо от правительства денежно-кредитную политику, назначая процентные ставки. Налогово-бюджетной политикой Ч налогами и расходами заведуют законодательные и исполнительные власти. Однако каждый из этих видов политики имеет разные цели. Центральный банк стремится ограничить рост предложения денег и обеспечить низкие темпы инфляции. Артур Берне, специалист по экономическим циклам и бывший глава ФРС, писал: лЧиновники центрального банка склонны, в силу традиции, а, возможно, и в силу личного склада, держать цены в узде. Их ненависть к инфляции еще более разгорается после общения с единомышленниками из частных финансовых кругов╗. Власти же, заведующие налогово-бюджетной политикой, больше озабочены такими вопросами, как полная занятость, собственная популярность, сохранение низких налогов и грядущие выборы.

Рис. 5 иллюстрирует результаты сочетания этих противоборствующих целей. Лица, проводящие налогово-бюджетную политику, предпочитают минимально возможную величину безработицы, увеличение государственных расходов в сочетании с понижением налогов и не заботятся об инфляции и частных инвестициях.

* - равновесие по Нэшу ! - кооперативное равновесие

Рис. 5. Недостаток координации приводит к малому объему инвестиций

В бюджетно-денежной игре кооперативная стратегия, изображенная в ячейке В, приводит к умеренной инфляции и безработице в сочетании с большим объемом инвестиций, стимулирующим экономический рост. Однако желание уменьшить безработицу и реализовать социальные программы побуждает руководство страны прибегать к увеличению бюджетного дефицита, тогда как неприятие инфляции заставляет центральный банк поднимать процентные ставки. Некооперативное равновесие в ячейке С означает наименьший возможный объем инвестиций

Они выбирают лбольшой бюджетный дефицит╗. С другой стороны, центральный банк пытается уменьшить инфляцию, не подвержен влиянию профсоюзов и лоббирующих группировок, и выбирает лвысокие процентные ставки╗. Результатом является некооперативное равновесие в ячейке С с умеренными величинами инфляции и безработицы, но с низким уровнем инвестиций.

Возможно, что именно благодаря лбюджетно-денежной игре╗ президент Клинтон выдвинул экономическую программу по уменьшению бюджетного дефицита, снижению процентных ставок и расширению объема инвестиций.

Игры, игры, везде игры...

В свете лтеории игр╗ можно рассмотреть экономику, общественные науки, бизнес и повседневную жизнь. К примеру, в экономике с точки зрения лтеории игр╗ можно объяснить торговые и ценовые войны. Кроме того, некоторые обозреватели полагают, что, используя эту теорию, можно показать причины такого феномена, как лмалоподвижные╗ цены. В соответствии с этой теорией, фирмы заключают нечто вроде тайного соглашения о преобладающем значении цены (скажем, если речь идет об автомобильной или сталелитейной промышленности). После того, как они пришли к соглашению, фирмы отказываются понижать

или повышать цены, так как в противном случае участники рынка будут рассматривать такие изменения как сигнал объявления экономической войны.

С помощью теории игр можно также объяснить, почему иностранная конкуренция может привести к более ожесточенной ценовой войне. Что случится, если японская фирма войдет на американский рынок, на котором уже существующие компании тайно договорились назначить высокую цену? Зарубежные фирмы могут лотказаться играть в эту игру╗. Они просто будут снижать цены в целях овладения большей долей рынка. Сговор может разрушиться.

Положение усложняется, когда люди пытаются лизменить игру╗, действуя нечестно или меняя величину выигрыша. Фирма может изменить объем выигрышей, получаемых потенциальным конкурентом .на ее рынке, построив большие производственные мощности, чем ей требуются. Такие действия предпринимаются для того, чтобы лобязать╗ себя назначить такие низкие цены, что потенциальный конкурент, установив их, не сможет заработать прибыль. Наиболее лстрашным╗ примером такого типа игры является лугроза судного дня╗ ядерных сверхдержав, при которой одна из держав грозится развязать войну, приводящую к взаимному уничтожению, если другая держава будет осуществлять менее агрессивные меры.

Эти несколько примеров иллюстрируют только часть огромного разнообразия результатов, которые можно получить, используя теорию игр. Данный раздел экономической теории является чрезвычайно полезным (для экономистов и других представителей общественных наук) инструментом анализа ситуаций, при которых небольшое число людей хорошо информировано и пытается перехитрить друг друга на рынках, в сфере политики или в военных действиях.